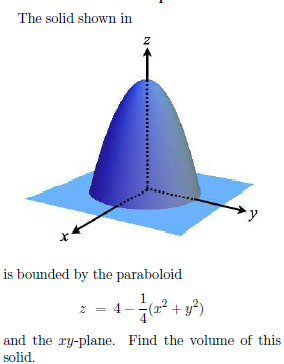
The Solid That Lies Below The Paraboloid Z 4 X2 Y2 Gauthmath
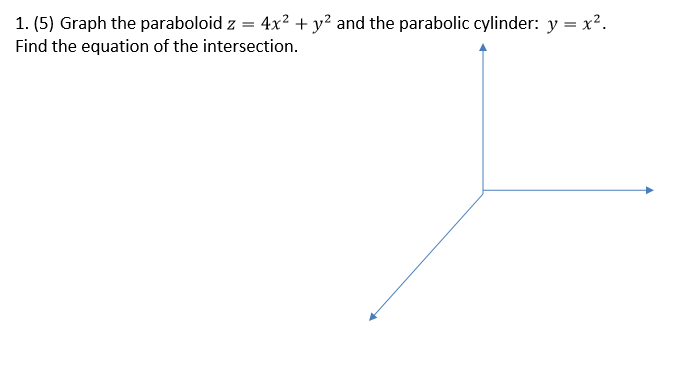
The plane xy2z=2 intersects the paraboloid in an ellipse Find the points on this ellipse that are nearest to and farthest from the origin Explanation Step 1Bounded between the planes z= 0 and z = 2 Evaluate x)dS (b) Let F be the vector field F = (xy, yz, zx) Let S denote the part of the paraboloid z = 4 – x2 – y?
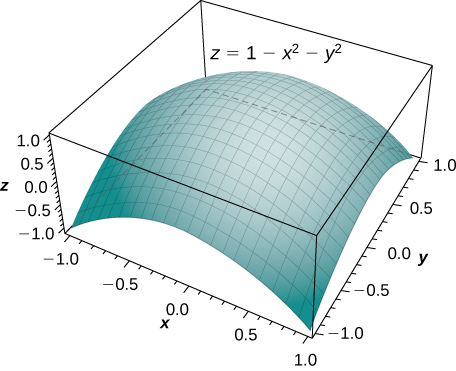
Paraboloid z=4-x^2-y^2
Paraboloid z=4-x^2-y^2-Answer to Let S be the portion of the paraboloid z = 4 x^2 y^2 lying on and above the xyplane a Find a parametrization, \\phi(u, v), of the5 comments share save hide
Macs Citadel Edu
(a) Let S be the surface z2 = x² y? Since 1st quadrant means x>0 and y>0 in 2D space, I guess 1st octant means x>0, y>0 and z>0 in 3d space The way I would do this is add up slices ie at any particular z value, work out the area A of the slice ie V = (integrate z from 0 to 8) A * dz At any z, the formula for the cross section plane is 2x^2 2y^2 = z 2(d) 6pt the part of the sphere x 2y 2z2 = 4z that lies inside the paraboloid z = x y Answer Rewrite equation of the sphere x 2 y (z − 2) = 4 The intersection curve is a circle z = 3;
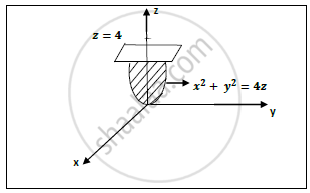
X2 y2 = 3 Thus domain D is 0 ≤ θ ≤ 2π, 0 ≤ r ≤ 3;Let E be the region bounded below by the r θ r θplane, above by the sphere x 2 y 2 z 2 = 4, x 2 y 2 z 2 = 4, and on the sides by the cylinder x 2 y 2 = 1 x 2 y 2 = 1 (Figure 554) Set up a triple integral in cylindrical coordinates to find the volume of the region using the following orders of integration, and in each case findFigure 1 Region S bounded above by paraboloid z = 8−x2−y2 and below by paraboloid z = x2y2 Surfaces intersect on the curve x2 y2 = 4 = z So boundary of the projected region R in the x−y plane is x2 y2 = 4 Where the two surfaces intersect z = x2 y2 = 8 − x2 − y2 So, 2x2 2y2 = 8 or x2 y2 = 4 = z, this is the curve at the intersection of the two surfaces
Paraboloid z=4-x^2-y^2のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
「Paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「Paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
「Paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 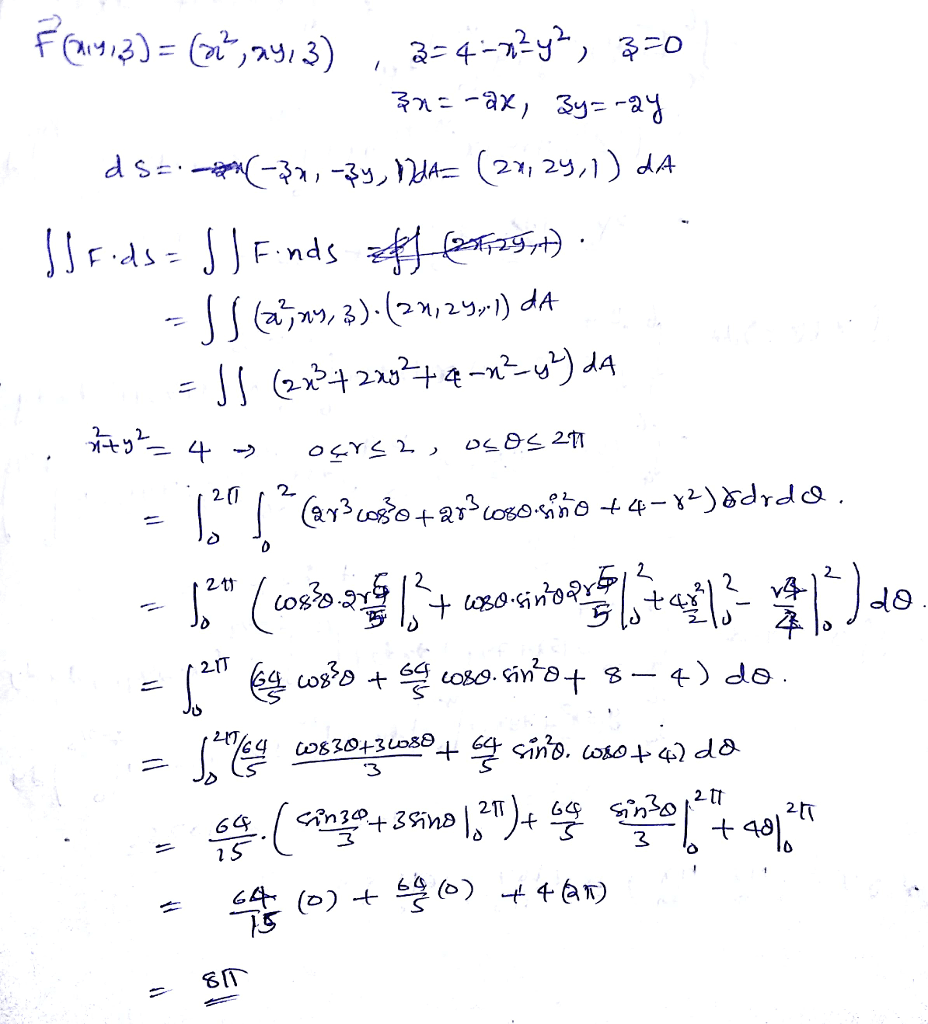 |  |
 | ||
「Paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「Paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 | ||
「Paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「Paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「Paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  | |
「Paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「Paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「Paraboloid z=4-x^2-y^2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
answered by Taniska (645k points) selected by Vikash Kumar Best answer Let A (3, –6, 4) and let P (x, y, z) be any point on the paraboloid x2 y2 – z = 0 AP2 = (x – 3)2 ( y 6)2 (z – 4)2 by distance formulaI have no idea how to even approach this or visualize it I tried integrating straightaway with the given x's and y's Help!




